Mathematische Grundlagen GIS

Begriffe

Polygon

Ein geschlossenes Vieleck, d.h. der erste Eckpunkt ist gleich dem letzten Eckpunkt. Es gibt 2D-Polygone (nur x,y-Koordinaten) und 3D-Polygone (mit x,y,z-Koordinaten)

Polygonschicht

Mathematisches Model eines Gelände-Polygons mit Bohrstellen, an denen die Schichtdicke gemessen wird.

Mathematisch ist eine Polygonschicht ein Volumen-Element, das in der Projektion von oben und von unten aus dem gleichen Polygon besteht. Es gibt weitere Punkte (Bohrstellen).

Liegt die Bohrstelle bezüglich der x,y-Koordinaten innerhalb des Projektionspolygons, gehört der Punkt zur Polygonschicht, sonst nicht.

sichtbarer Punkt

Gegeben ein (Eck-)Punkt Q und eine Menge M von Punkten Px. Ein Punkt Pn ist dann von Punkt Q aus sichtbar,

wenn für alle Geraden durch Pa und Pb mit a != n und b != n und a != b gilt: Die Punkte Q und Pn liegen auf der gleichen Seite der Geraden.

Anderst formuliert: Ein Punkt Pn ist vom Eckpunkt Q aus sichtbar, wenn die Punkte Pn und Q auf der gleichen Seite jeder Geraden liegen, die durch die restlichen Punkte aus M definiert werden.

Beispiele: (siehe untere Graphik): Von P1 aus sind B1 und B2 sichtbar, B3 ist nicht sichtbar, da von B3 auf der anderen Seite der Gerade B1/B2 ist wie P1.

Von P2 aus sind ebenfalls B1 und B2 sichtbar

Deckfläche

Die 3D-Fläche, die bei einer Sicht von oben sichtbar ist.

Bodenfläche

Die 3D-Fläche, die bei einer Sicht von unten sichtbar ist.

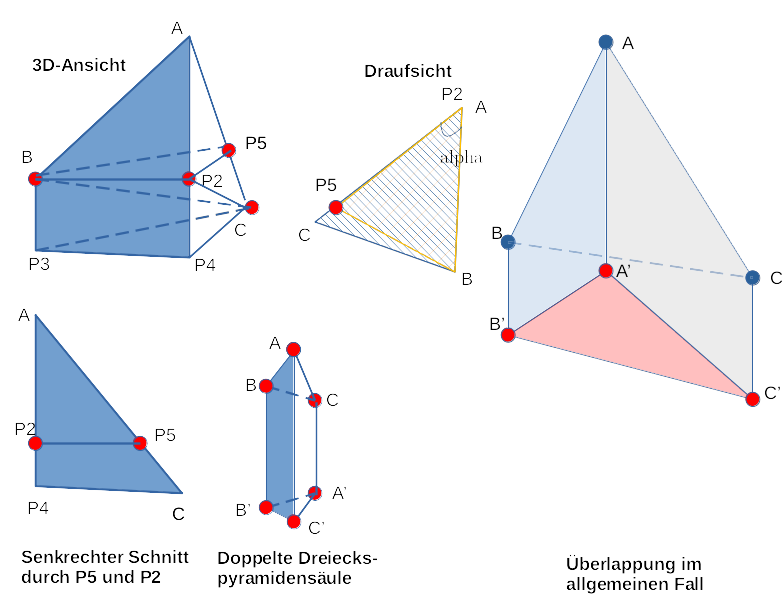
Dreieckspyramidensäule

Ein 3D-Objekt mit einem Dreieck als Grundfläche. Von den Ecken dieses Dreiecks führen drei senkrechte Kanten nach oben, die in drei Punkten enden.

Diese drei Punkte bilden wieder ein Dreieck, die Deckfläche.

Wenn es einen höchsten Punkt gibt (z-Koordinate dieses Punktes ist größer als die z-Koordinaten der andern), sieht das wie eine Dreieckspyramide aus.

Sieht man sich die Figur genauer an, besteht sie aus 3 Körpern: einem Prisma, einem Pyramidenstump und einer Dreieckspyramide. Näheres siehe Herleitung Volumenformel

Mathematische Basis

Herleitung der Volumenformel

• Koordinatenangaben: zX bedeutet z-Koordinate von Punkt X, entsprechend xB ist die x-Koordinate von Punkt B, yP der y-Wert von Punkt P.
• A ist der Punkt mit dem maximalen z-Wert
• C ist der Punkt mit dem minimalen z-Wert
• B ist der dritte Punkt, also dem dazwischenliegenden z-Wert
• P3 ist der Projektionspunkt unter B, also mit gleichen x,y-Kordinaten wie B und der z-Koordinate von C
• P4 ist der Projektionspunkt unter A, also mit gleichen x,y-Kordinaten wie A und der z-Koordinate von C
• P2 und P5 entstehen, wenn eine "waagrechte" Ebene durch den Punkt B gezogen wird, wobei P2 auf der Gerade A/P4 liegt, und P5 auf der Gerade A/C
• Die Dreieckspyramidensäule besteht aus 4 Teilen (von unten nach oben):
  • ein Prisma mit Grundfläche A0 und Höhe h = zC - zPlane, wobei zPlane die z-Koordinate der Grundfläche ist. V = A0*h. Hinweis: nicht in "3D-Ansicht" zu sehen. Wäre die jeweilige senkrechte Verlängerung von P3, P4 und C nach unten.
  • einem Keil mit Grundfläche area0 (P3, P4 und C) und der Oberkante B und P2
  • einer Pyramide mit Grundfläche area1 (B, P2, P5) und darunterliegender Spitze C.
  • einer Pyramide mit Grundfläche area1 (B, P2, P5) und der Spitze A

Berechnung der Fläche area1

• Sei P3 der Projektspunkt von B auf die Ebene z=zC, also (x, y) von B und z von C
• Sei P4 der Projektspunkt von A auf die Ebene z=zC, also (x, y) von A und z von C
• Siehe Grafik Senkrechten Schnitt durch P5 und P2
  • Es gilt der Strahlensatz: Sei d25 der Abstand P2/P5, d4C der Abstand P4/C:
  • Strahlensatz: d25 / d4C = (zA - zB) / (zA - zC)
  • d25 = (zA - zB) / (zA - zC) * d4C
  • Abstand P4/C (d4C) ist der Abstand von A und C in der Projektionsebene (ohne Berücksichtigung der z-Koordinate): d4C = sqrt((xA - xC)² + (yA - yC)²)
• Aus der Grafik Draufsicht, großes Dreieck, ergibt sich:
  • alpha ist der Winkel bei Punkt A: Für die drei Seiten a, b, c und den Winkel alpha gilt:
    Cosinussatz: a² = b² + c² - 2 * b * c * cos(alpha)
  • cos(alpha) = (b² + c² - a²) / (2 * b * c)
  • Im Dreieck Projektion A B C (siehe Draufsicht): dbc ist Abstand B/C, dac ist Abstand A/C und dab ist Abstand A/B
  • dbc = sqrt(xB -xC)² + (yB - yC)²), dac = sqrt((xA - xB)² + (yA - yB)²), dab = sqrt((xA - xB)² + (yA - yB)²)
  • cos(alpha) = (dac² + dab² - dbc²) / (2 * dac * dab)
  • Der Abstand d5b (Abstand P5 / B) ergibt sich aus dem Cosinussatz (kleines Dreieck in der Draufsicht):
    • a²=b² + c² - 2 * b * c * cos(alpha)
    • a = d5b, b = d25, c = dab
    • d25 ist der Abstand P2/P5, dab der Abstand A/B, alpha der Winkel an A
    • d5b² = d25² + dab² - 2 * d25 * dab * cos(alpha)
    • d5b = sqrt(d25² + dab²- 2 * d25 * dab * cos(alpha))
  • Fläche nach Satz von Heron:
    Für die Seiten a, b, c eines Dreiecks gilt: s=(a + b + c)/2
    A = sqrt(s*(s-a)*(s-b)*(s-c))
    • s = (dab + d5b + d25) / 2
    • area1 = sqrt(s*(s-a)*(s-b)*(s-c))

Volumen des Keils P3, P4, C, B und P2

• V1 = area0 * h1 * 1/2, wobei h1 der Abstand von P2/P4 ist: h1 = zB - zC
• V1 = area0 * (zB -zC) / 2

Volumen der unteren Pyramide (B, P2, P5, C)

• V2 = area1 * h1 / 3
• V2 = area1 * (zB - zC) / 3

Volumen der oberen Pyramide B, P2, P5, A

• V3 = area1 * h2 / 3
• h2 ist der Abstand P2 und A, also zA-zB
• V3 = area1 * (zA - zB) / 3

Gesamtvolumen des Geländemodells

• Das Geländemodell enthält gegenüber einem allgemeinen Polyeder Vereinfachungen, die die Berechnung erleichtern:
• Für jede Schicht gilt: Jedem Punkt der Deckfläche ist ein darunterliegender Punkt der Bodenfläche zugeordnet.
• Trianguliert man die Punkte der Deckfläche, so ergeben aus den jeweils drei Punkten der Deckfläche und den zugeordneten drei Punkten der Bodenfläche eine "doppelte" Dreieckspyramidensäule, eine mit nach oben gerichteter Spitze in der Deckfläche und eine mit nach unten gerichteter Spitze in der Bodenfläche (siehe obige Graphik).
• Das Volumen der Schicht ergibt die Summe der Volumina dieser doppelten Dreieckspyramidensäulen.
• Die Berechnung der nach oben liegenden Spitze ist oben gezeigt.
• Sei A' der Punkt des Bodendreicks mit der höchsten z-Koordinate, C' der mit der niedrigsten und B' der mit der mittleren z-Koordinate.
• Die gleiche Berechnung kann für die untere Spitze benutzt werden, wenn die Spitze an der Ebene z=0' gespiegelt wird (z-Koordinate wird mit -1 multipliziert).
• Die Länge des Dreiecksprismas zwischen den Spitzen ist zC - zA'
• Bleibt noch der Sonderfall Überlappung, wenn zC - zA' negativ wird, wenn also A' oberhalb von C liegt.

Berechnung bei Überlappung

• Da A' immer unterhalb A liegt, B' unter B und C' unter C, ergibt sich hier immer ein (meist schiefwinkliges) "Tortenstück", wobei der dreieckige Deckel immer oberhalb des dreieckigen Bodens liegt.
• Wir führen eine Grundebene ein mit z=zC'. Da C' immer der unterste Punkt ist, liegen alle anderen Punkte oberhalb oder in dieser Ebene.
• Betrachtet man das 3D-Objekt "Deckel" aus der Deckfläche (A, B und C und der Grundebene, sieht man eine Dreickspyramidensäule.
• Betrachtet man das 3D-Objekt "Boden" aus der Bodenfläche (A', B' und C' und der Grundebene, sieht man eine Dreickspyramidensäule (ohne Prisma).
• Das Volumen des Tortenstücks ergibt sich aus der Differenz von Volumen-Deckel und Volumen-Boden.

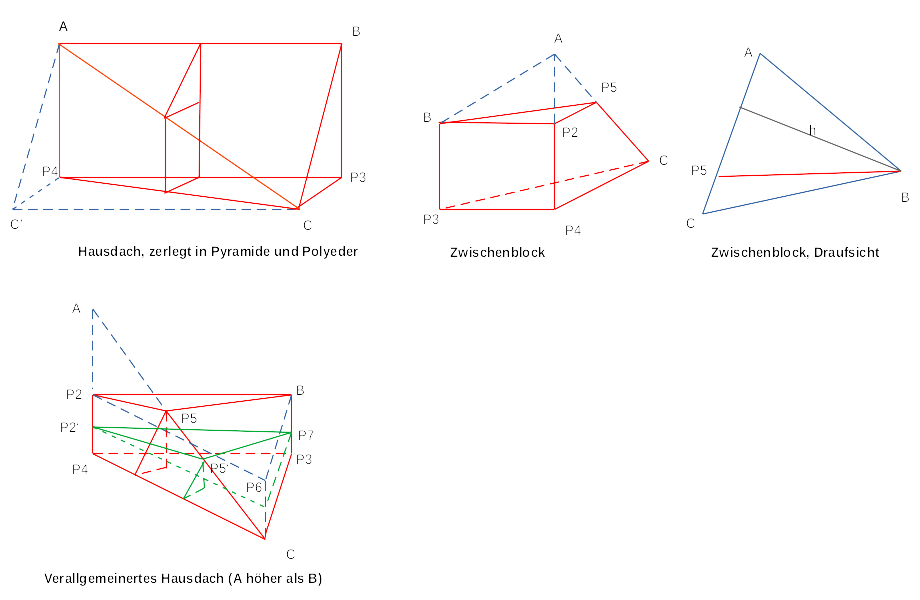
Sonderfall "Hausdach"

Wir schauen uns eine 3D-Figur an, die einem halben "Hausdach" entspricht. Wir schneiden die Figur senkrecht durch zwei diagonale Punkte der Grundfläche. Damit zerlegen wir die Grundfläche in 2 kongruente Dreiecke. Es entsteht eine Pyramide und ein "komplizierterer" Polyeder.

• Das Volumen des Polyeders C P3 P4 A B bildet zusammen mit der Pyramide C C' P4 A ein "Hausdach"
• Das Volumen des Polyeders muss das 2-fache Volumen der Pyramide haben:
  • Gleiche Grundfläche area0: C P3 P4 ist kongruent zu C' P4 C
  • Volumen Hausdach: 1/2 * h * area0 * 2 Hinweis: Grundfläche ist das Rechteck aus beiden Dreiecken
  • Volumen Pyramide: 1/3 * h * area0
  • Volumen Polyeder = 2 * 1/2 * h * area0 - 1/3 * h * area0 = 2/3 * h * area0

Formel Zwischenblock

Hinweis: Die Ansichten "Zwischenblock" und "verallgemeinertes Hausdach" zeigen das gleiche 3D-Objekt, nur aus verschiedener Kameraposition: Beim "Zwischenblock" ist der Punkt C im Hintergrund, beim "verallgemeinertes Hausdach" im Vordergrund.

• Dreieck (A B C) hat die gleiche Höhe h wie (A P5 B). Sei da5 Abstand A / P5, dac Abstand A / C.
  • area1 = da5 * h / 2, area0 = dac * h / 2
  • area1 / area0 = da5 / dac
  • area1 = area0 * da5 / dac
• Strahlensatz: siehe "Zwischenblock"
  • Sei h1 der Abstand P4 / P2, d5a der Abstand P5 / A, h0 der Abstand A / P4, da2 der Abstand A / P2, dac der Abstand A / C:
  • da2 / h0 = da5 / dac
  • da5 = da2 * dac / h0
  • Es gilt: h1 + da2 = h0, da2 = h0 - h1
  • da5 = (h0 - h1) * dac / h0
  • Setzt man die obige Flächenformel ein:
  • area1 = area0 * da5 / dac = area0 * (h0 - h1) * dac / (h0 * dac)
  • area1 = area0 * (h0 - h1) / h0
  • Es gilt also für die Fläche area1 in Abhängigkeit von Höhe h die Funktion A(h) = area0 * (h0 - h) / h0
• Das Volumen des Zwischenblocks ist die Integration von A(h) von 0 bis h1:
  • V = integral(0-h1, area0 * (h0 - h) / h0 * dh)
  • V = area0 / h0 * integral(0-h1, (h0 - h) * dh)
  • Berechnen des spannenden Teils mit "normaler" Benennung x statt h:
  • Stammfunktion F(x) = integral(h0 - x) * dx)
  • F(x) = h0 * x - 1/2 * x² + C
  • Kontrolle: F'(x) = h0 - 2*1/2*x = h0 - x
  • Berechnen des bestimmten Integrals von 0 bis h1:
  • V = area0 * 1/h0 * (h0*h1 - 1/2(h1²))

Grenzwerte

• Ist h1 0, ist V auch 0: korrekt
• Geht h1 gegen h0 (A auf gleicher Höhe wie B):
• V = area0 * 1/h0 (h0² - 1/2 h0²) = area0 * h0 * 1/2. Das ist das Volumen des entstehenden Keils, korrekt.

Gewichteter Mittelwert (wird im vereinfachten Modell nicht benutzt)

Der gewichtete Mittelwert soll dafür sorgen, dass weiter entfernte Punkte weniger Einfluss haben als nähere Punkte.

Dies wird durch den reziproken Wert des Abstands erreicht.

Die Summe der Gewichtsfaktoren muss 1 (dem neutralen Element der Multiplikation) sein.

Sei ax der Abstand des Punktes Qx von P und F ein Gewichtsfaktor, dann gilt:

1 = (F/a1 + F/a2 + ... F/an)

Umgeformt ergibt das:

F = 1/(1/a1 + 1/a2 + ... 1/an)

Formel für das gewichtete Mittel:

z = F*(z1/a1 + z2/a2 + ... + zn/an)

Schichtenmodell

Zielsetzung

Es sollen die Volumina einer Menge von übereinanderliegenden Polygonschichten bestimmt werden können. Dabei sind nur eingeschränkte Informationen über die tatsächliche Geometrie vorhanden. Daher müssen fehlende Informationen durch Interpolation bestimmt werden.

Vereinfachtes Modell

• Geländepolygon:
  • Es wird vereinbart, dass das Modell nur aus den Bohrstellen bestimmt wird.
  • Damit besteht das Polygon aus der konvexen Hülle (der "Umrisslinie") der Koordinaten der Bohrstellen.
  • In diesem vereinfachten Modell ist keine Interpolation des Geländepolygons mehr notwendig, da die Koordinaten aus den Messungen (Koordinaten der Bohrstelle, Höhe der Schicht) gegeben sind.
• Schichten
  • Alle Messpunkte haben die gleiche Anzahl Schichten in der gleichen Reihenfolge, wobei Schichthöhe von 0 bedeutet, dass die Schicht an dieser Bohrstelle nicht vorkommt.
  • Aus den realen Daten der Bohrstellen muß diese Schichtstruktur durch passende Erweiterung erstellt werden

Beispiel Schichtenbehandlung

• Bohrstelle B1 hat Schichten A, B und C mit den Höhen 2 2.5 und 3
• Bohrstelle B2 hat Schichten B, A, C, D mit den Höhen 3.5, 4, 4.5 und 5

Dann ergibt sich folgende Schichtstruktur:

• Schicht S1 ist Schicht A von B1
• Schicht S2 ist die Schicht B von B1 und gleichzeitig Schicht B von B2
• Schicht S3 ist die Schicht A von B2
• Schicht S4 ist die Schicht C von B1 und die Schicht C von B2
• Schicht S5 ist die Schicht D von B2
• Die Tiefen von B1 sind S1: 2 S2: 2.5 S3: 0 S4: 3 S5: 0
• Die Tiefen von B2 sind S1: 0 S2: 3.5 S3: 3.5 S4: 4.5 S5: 5

Interpolation der Schichtpolygone (im vereinfachten Modell nicht notwendig)

Es sind die 3D-Daten des obersten Geländepolygons vorhanden. Dazu kommen die 3D-Daten der Bohrstellen und die Höhenangaben der Schichten aus den Bohrstellen.

Für die Volumenberechnung werden die z-Koordinaten des Polygons benötigt:

• Im obersten 3D-Polygon sind die z-Koordinaten bekannt.
• In der obersten Polygonschicht wird die Deckfläche durch das Polygon und die Bohrpunkte, die innerhalb des Polygons liegen, bestimmt.
• In der n-ten Polygonschicht ist die Deckschicht die Bodenschicht der (n-1)-ten Polygonschicht.
• Die n-te Bodenschicht: Die z-Koordinate jedes Polygon-Eckpunktes werden so interpoliert: Es werden alle sichtbaren Bohrpunkte bestimmt. Die z-Komponente jedes Polygonecks ergibt sich aus dem gewichteten Mittelwert der z-Koordinaten der sichtbaren Bohrpunkte.